Prologue: The Illusion of Prosperity

In the early 2000s, the United States and much of the Western world were riding high on a wave of economic prosperity. The stock market was booming, home prices were soaring, and credit was available to almost anyone who wanted it. The American Dream had never seemed more attainable. But beneath the surface, cracks were forming in the foundations of this seemingly unstoppable growth.

Act 1: The Bubble Inflates (2000-2006)

The origins of the Great Recession can be traced back to a combination of financial deregulation, a booming housing market, and risky lending practices.

• The Role of Subprime Mortgages:
  • Banks and financial institutions, encouraged by deregulation, began issuing high-risk loans to borrowers with poor credit histories.
  • The subprime mortgage market grew from 8% of total mortgage originations in 2001 to over 20% by 2006.
  • Mortgage-backed securities (MBS) and collateralized debt obligations (CDOs) turned these risky loans into attractive investments.

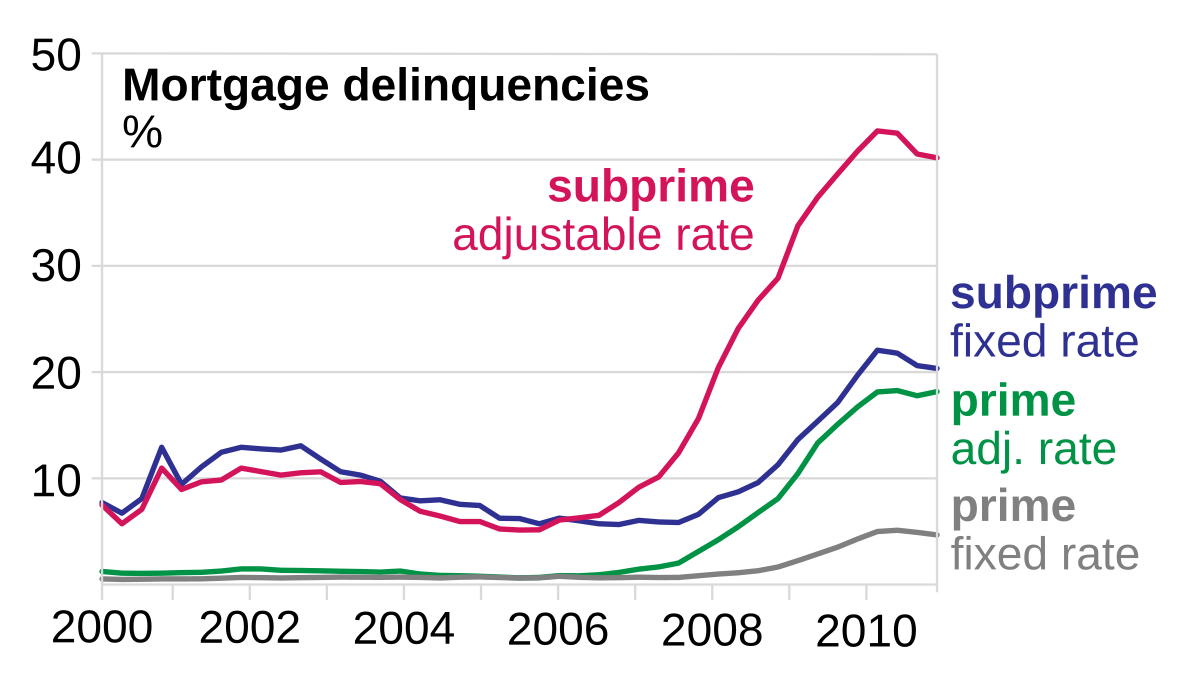
• The Role of the Federal Reserve:
  • In response to the dot-com bubble burst in 2000, the Federal Reserve lowered interest rates from 6.5% in 2000 to 1% by 2003.
  • Cheap credit fueled an artificial boom in housing, encouraging speculative investments.

• Wall Street’s Greed and Financial Engineering:
  • Major banks and financial institutions, including Lehman Brothers, Bear Stearns, and AIG, aggressively pushed for the sale of MBS and CDOs.
  • Credit rating agencies, such as Moody’s and Standard & Poor’s, assigned AAA ratings to these risky securities, falsely signaling their safety to investors.

In the bustling streets of Glasgow, Scotland, in the 1870s, a young, ambitious entrepreneur named Sir Thomas Lipton had a vision—to make tea, once a luxury for the elite, accessible to everyone. Little did he know that his dream would evolve into a global tea empire that would redefine the industry for generations to come.

The Humble Beginnings

Thomas Lipton, born in 1848 to Irish immigrant parents, was no stranger to hard work. At the age of 15, he sailed to the United States, where he took up various jobs, including working in a grocery store. Observing the efficiency of American retail operations, he returned to Scotland with a dream of revolutionizing the food trade.

In 1871, at the age of 23, Lipton opened his first grocery store in Glasgow. He marketed his store as offering “the best goods at the cheapest prices,” a philosophy that won the hearts of working-class families. His business grew rapidly, and by the 1880s, he owned over 300 stores across Britain. But Lipton was always thinking bigger.

Introduction to Explainable AI (XAI)

Explainable AI (XAI) refers to the subset of artificial intelligence focused on making the decisions and predictions of AI models understandable and interpretable to humans. As AI systems grow in complexity, particularly with the use of deep learning, their “black-box” nature poses challenges in trust, accountability, and regulatory compliance. XAI techniques aim to bridge this gap by providing insights into how AI models make decisions.

Source: Internet

Key Components of XAI

Model Interpretability:

• Ability to understand the inner workings of an AI model.
• Examples: Decision trees, linear regression, and simple neural networks are inherently interpretable.

Post-Hoc Explanations:

• Techniques that explain the decisions of black-box models without altering their architecture.
• Examples: LIME (Local Interpretable Model-Agnostic Explanations), SHAP (SHapley Additive exPlanations).

Machine learning frameworks and technologies continue to evolve, leading to the rise of competing platforms designed to maximize performance, flexibility, and ease of use for modern AI workloads. Two prominent frameworks, MLX (Machine Learning Exchange) and CUDA (Compute Unified Device Architecture), are often compared in terms of performance and functionality. This article provides a detailed exploration of the differences between MLX and CUDA, focusing on their architecture, usability, and benchmarking scores.

What is CUDA?

CUDA is a parallel computing platform and programming model developed by NVIDIA, specifically designed for NVIDIA GPUs. It allows developers to use C, C++, Fortran, and Python to write applications that can leverage GPU acceleration. CUDA provides low-level access to the GPU hardware, enabling high performance for applications like deep learning, scientific computing, and high-performance simulations.

Source: Internet

Key features of CUDA:

• Low-level optimization: Offers direct control over GPU memory and thread management.
• Rich ecosystem: Integrated with libraries like cuDNN, NCCL, and TensorRT.
• Highly mature: Over a decade of optimizations and wide industry adoption.

Apache Airflow is a powerful open-source platform used to programmatically author, schedule, and monitor workflows. It is designed for complex data engineering tasks, pipeline automation, and orchestrating multiple processes. This article will break down Airflow’s architecture and provide a code example to help you understand how to work with it.

Source: Internet

Key Concepts in Airflow

Before diving into the architecture, let’s go over some important Airflow concepts:

• DAG (Directed Acyclic Graph): The core abstraction in Airflow. A DAG represents a workflow, organized as a set of tasks that can be scheduled and executed.
• Operator: A specific task within a DAG. There are various types of operators, including PythonOperator, BashOperator, and others.
• Task: An individual step in a workflow.
• Executor: Responsible for running tasks on the worker nodes.
• Scheduler: Determines when DAGs and their tasks should run.
• Web Server: Provides a UI for monitoring DAGs and tasks.
• Metadata Database: Stores information about the DAGs and their run status.